수치해석 실습 101#
강좌: 수치해석
낙하산병 문제#
낙하산을 맨 병사는 중력과 공기에 의한 항력을 받는다.

Fig. 1 낙하산병 (From pxhere.com)#
이 때 사람에 작용하는 힘은 다음과 같다.
여기서 \(F_D\) 중력에 의해 아래 방향으로 작용하는 힘이고 \(F_U\) 는 공기 저항에 의해 위로 작용하는 힘이다. 각각은 다음과 같이 표현할 수 있다.
여기서 \(m\) 은 질량, \(g\) 는 중력 가속도이다. \(c\)는 항력 계수이고, \(v\) 는 속도이다.
뉴턴의 제2법칙을 적용하면 지배방정식 (Governing Equation)은 다음과 같다.
엄밀해 결과 가시화#
낙하산병이 처음에 정지하고 있었다면 (\(t=0\) 일 때 \(v=0\)), 이 미분방정식의 엄밀해 (Exact Solution) 은 다음과 같다.
낙하산 병의 몸무게 \(m=68.1 kg\), 항력계수 \(c=12.5 kg/s\)로 생각하자. 중력 가속도는 \(9.81 m/s^2\)으로 가정하자.
파이썬에서는 matplotlib 패키지로 그래프를 그린다. 아래와 같이 불러온다.
Jupyter 노트북 내 실행을 위한 매직 커맨드
%matplotlib inline또는%matplotlib notebook
pyplot모듈 불러오기Matlab과 비슷하게 그래프를 그릴 수 있는 interface
그래프 스타일 로드
그림 DPI 조절
%matplotlib inline
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150
엄밀해를 계산하는 함수를 만들어보자.
import numpy as np
# 주요 상수
m = 68.1
c = 12.5
g = 9.81
# 엄밀해 계산 함수
def exact(t):
return g*m/c*(1-np.exp(-(c/m)*t))
exact(10)
44.91892648723751
시간에 따른 엄밀해를 30초 까지 연속적으로 계산해보자.
np.linspace 를 이용하면 등간격으로 시간을 구할 수 있다.
# 0~30 까지를 100 등분 함
t = np.linspace(0, 30, 101)
For Loop를 이용하면 연속적인 계산이 가능하다.
v = []
for ti in t:
v.append(exact(ti))
Pythoniac 코딩으로 List Comprehension을 사용하면 좀 더 빠르게 계산할 수 있다.
v = [exact(ti) for ti in t]
numpy 는 벡터 연산이 가능하므로 다음과 같이 빠르게 계산할 수 있다.
v = exact(t)
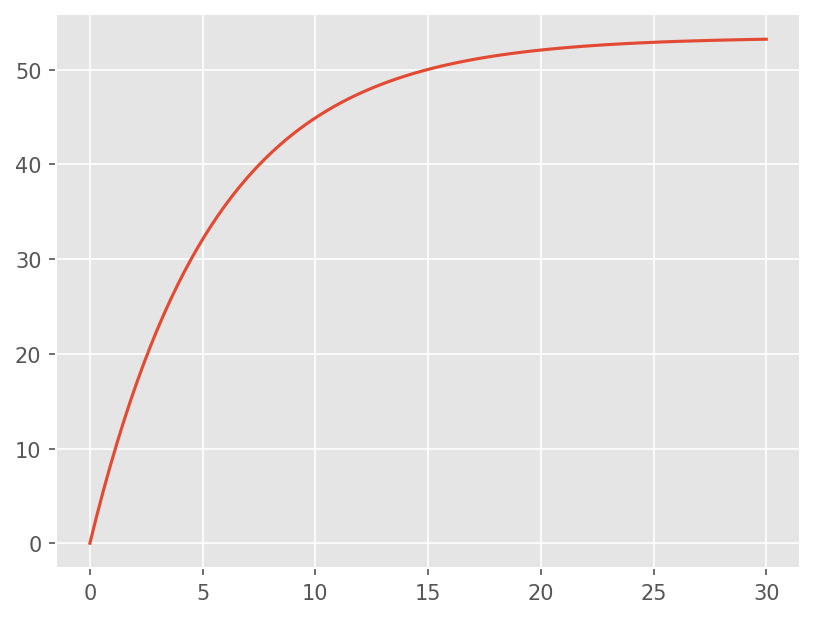
plt.plot 을 이용해서 그래프를 그리자
plt.plot(t, v)
[<matplotlib.lines.Line2D at 0x7f701e117610>]
Note
엔지니어는 그래프의 축과 선의 의미를 꼭 표기해야 한다. (무조건 오답 처리)
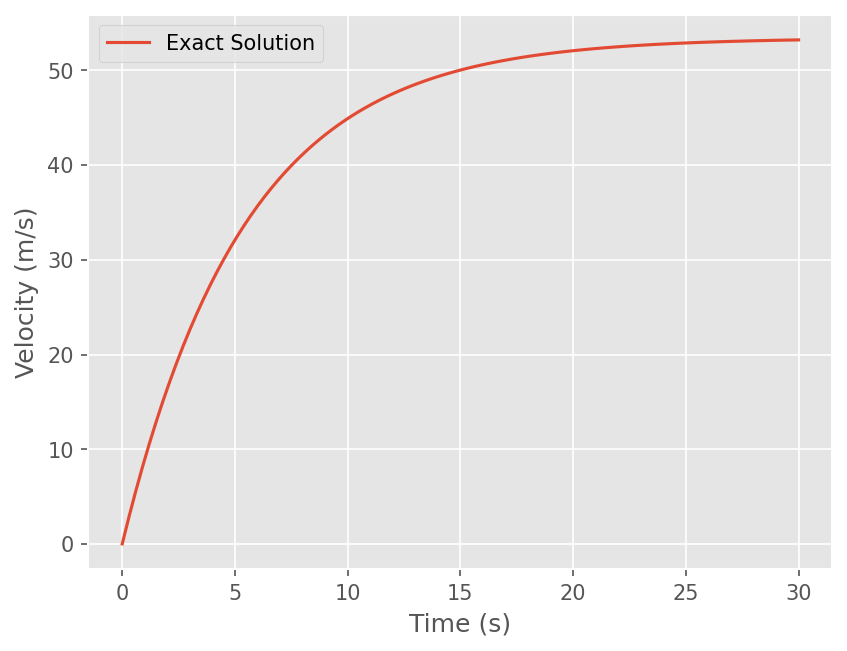
plt.plot(t, v)
# x,y 축 이름
plt.xlabel('Time (s)')
plt.ylabel('Velocity (m/s)')
# 그래프 선 이름
plt.legend(['Exact Solution'])
<matplotlib.legend.Legend at 0x7f701e193490>
수치해석#
이를 수치적으로 풀어보자. scipy 패키지에는 다양한 과학함수와 수치해석 기법을 제공한다.
scipy.integrate 에 있는 solve_ivp 함수로 계산해보자.
# solve_ivp 함수 호출
from scipy.integrate import solve_ivp
#solve_ivp?
# 우변 함수 작성
def f(t, v):
return g - c/m*v
sol = solve_ivp(f, [0, 30], [0])
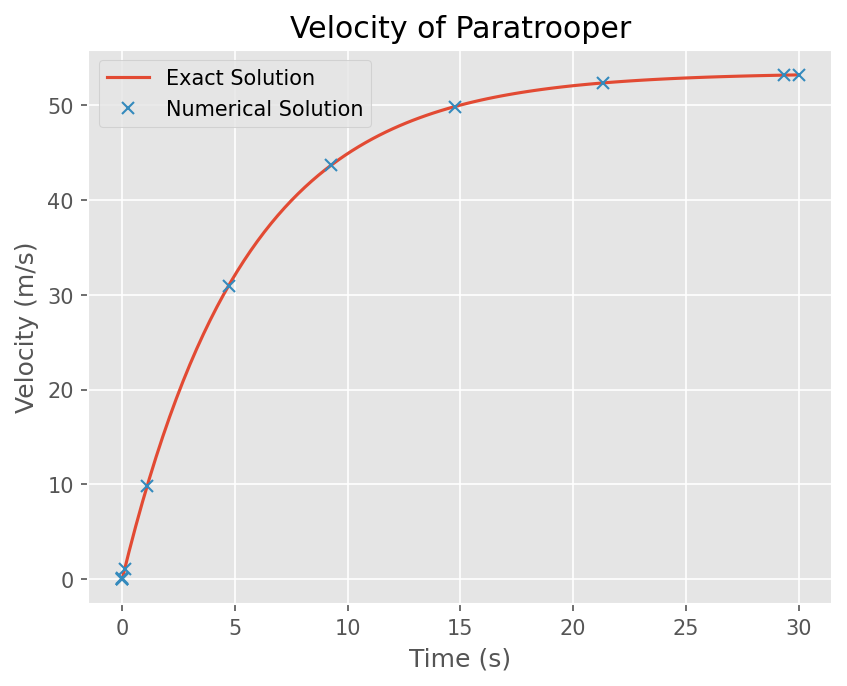
plt.plot(t, v)
# 수치해 결과 그리기 (Marker만 그리기)
plt.plot(sol.t, sol.y[0], linestyle='None', marker='x')
# x,y 축 이름
plt.xlabel('Time (s)')
plt.ylabel('Velocity (m/s)')
# 그래프 선 이름
plt.legend(['Exact Solution', 'Numerical Solution'])
# 그래프 이름
plt.title('Velocity of Paratrooper')
# 그래프 저장
plt.savefig('velocity.png', dpi=200)
Note
수치해석은 모든 답을 줄까? No !!! (No free lunch!!!)
계산 결과를 저장하자.
ASCII 방식과 Binary 방식이 있다.
ASCII data: 사람이 읽을 수 있도록 숫자, 문자, 기호로 표기
Binary data: 컴퓨터가 저장하는 2진수 방식으로 기록
행렬 (Array)를 어떻게 구분할까?
Whitespace (띄어쓰기, Tab)
# 데이터: (시간, 값) 으로 기록
arr = np.array([sol.t, sol.y[0]]).T
arr
array([[0.00000000e+00, 0.00000000e+00],
[1.00000000e-04, 9.80990997e-04],
[1.10000000e-03, 1.07899107e-02],
[1.11000000e-02, 1.08780146e-01],
[1.11100000e-01, 1.07885319e+00],
[1.11110000e+00, 9.86025483e+00],
[4.72197940e+00, 3.09793935e+01],
[9.26404220e+00, 4.36818913e+01],
[1.47507404e+01, 4.98740638e+01],
[2.13260752e+01, 5.23714367e+01],
[2.93351884e+01, 5.31924207e+01],
[3.00000000e+01, 5.32214224e+01]])
numpy 에 savetxt, loadtxt 함수를 활용하자.
# sol.csv 파일로 기록
np.savetxt('sol.csv', arr, delimiter=',', header='t,v', comments='')
# 확인 (Excel 에서도 읽기 가능)
with open('sol.csv') as f:
print(f.read())
t,v
0.000000000000000000e+00,0.000000000000000000e+00
9.999999999999999124e-05,9.809909967511212543e-04
1.100000000000000066e-03,1.078991067353642086e-02
1.110000000000000049e-02,1.087801455912157239e-01
1.111000000000000043e-01,1.078853190808823914e+00
1.111099999999999977e+00,9.860254828888242784e+00
4.721979401067658344e+00,3.097939353875368340e+01
9.264042202257618541e+00,4.368189129769811530e+01
1.475074044342309776e+01,4.987406378138719276e+01
2.132607522137336886e+01,5.237143665039166507e+01
2.933518837367320486e+01,5.319242067027523291e+01
3.000000000000000000e+01,5.322142241925892847e+01